simpletex一个好用的math工具

大家好，我是SimpleTex工具的开发者。当初决定开发SimpleTex，因为在市面上很难找到一款既好用又适合学生使用的LaTeX公式识别软件。我希望SimpleTex工具能为研究人员和学生提供便利，从我的个人研究项目起步，逐步发展为更加成熟的软件平台，为科技进步贡献自己的力量。

——https://simpletex.cn/about

确实非常好用，可以利用截图工具截取公式，然后直接复制到网页端或者客户端（APP），之后会自动识别为公式，并提供多种复制方式，应用领域很广泛！！！

实际案例

首先是目标公式

来源2026年高考一轮复习常用逻辑用语002（关于任意性与存在性问题的记忆方法——转化与化归）（已保留水印）

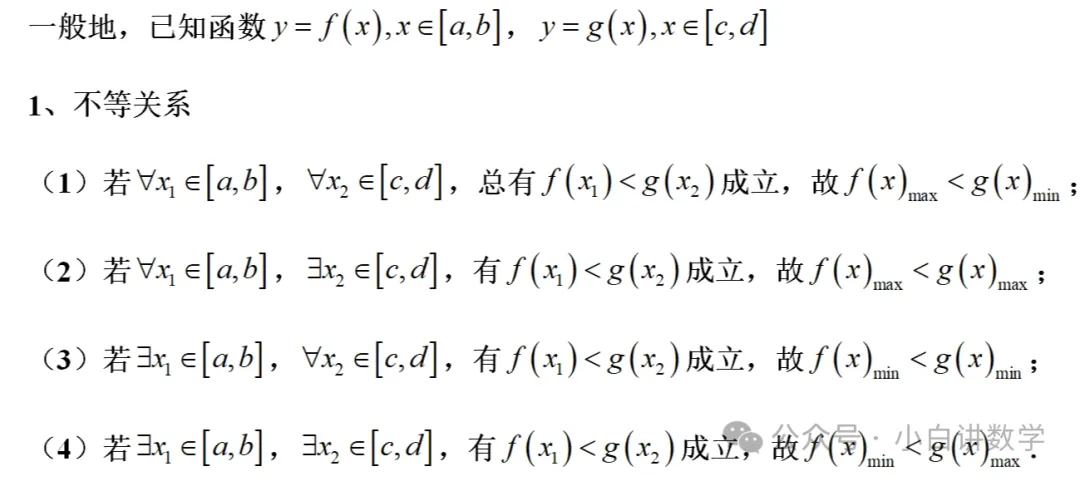
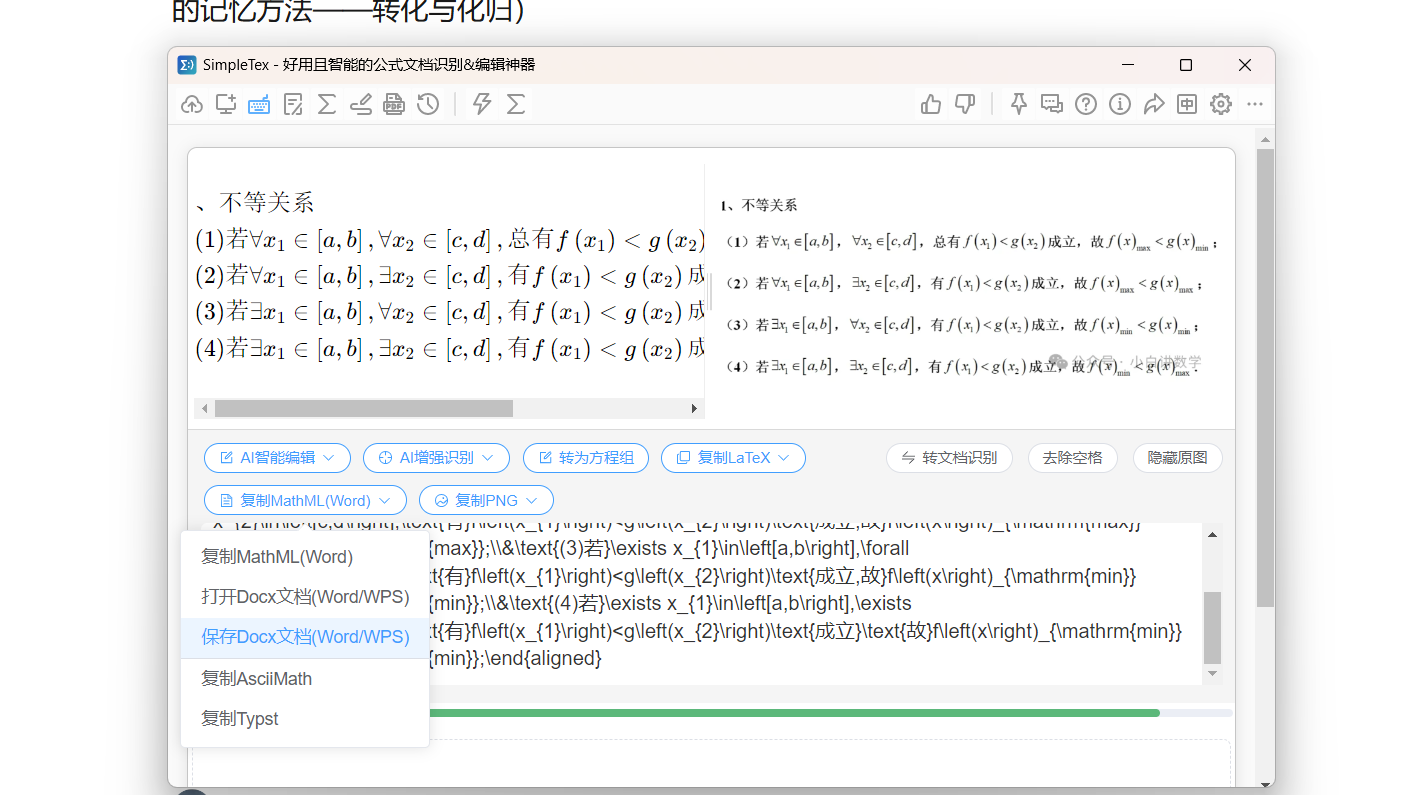
直接复制到网页端

https://simpletex.cn/ai/latex_ocr

然后，AI开始识别

然后是输出结果

1、不等关系

(1) 若 ∀x₁ ∈ [a,b], ∀x₂ ∈ [c,d], 总有 f(x₁) < g(x₂) 成立, 故 f(x)ₘₐₓ < g(x)ₘᵢₙ;

(2) 若 ∀x₁ ∈ [a,b], ∃x₂ ∈ [c,d], 有 f(x₁) < g(x₂) 成立, 故 f(x)ₘₐₓ < g(x)ₘᵢₙ;

(3) 若 ∃x₁ ∈ [a,b], ∀x₂ ∈ [c,d], 有 f(x₁) < g(x₂) 成立, 故 f(x)ₘᵢₙ < g(x)ₘᵢₙ;

(4) 若 ∃x₁ ∈ [a,b], ∃x₂ ∈ [c,d], 有 f(x₁) < g(x₂) 成立, 故 f(x)ₘᵢₙ < g(x)ₘᵢₙ.

相当的完美，没有错误

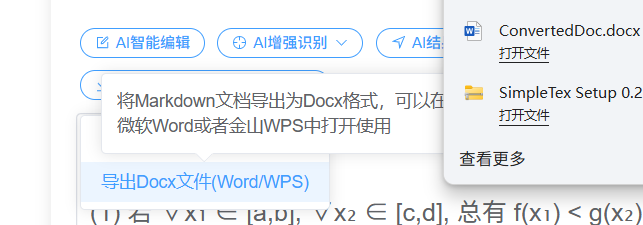
之后你还可以直接复制到文档DOCX或者下载

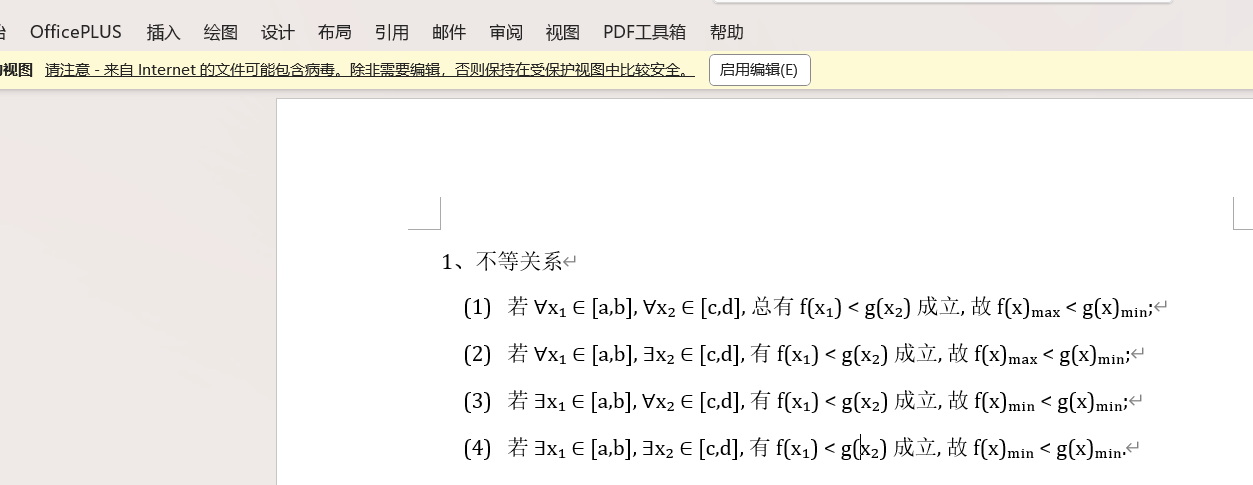
你还可以直接在客户端

软件在右下方SimpleTex

还是刚才的图

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mtable displaystyle="true" columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em" rowspacing="3pt">
    <mtr>
      <mtd>
        <mrow>
          <mrow>
            <maligngroup/>
          </mrow>
          <mrow>
            <maligngroup/>
            <mtext>、不等关系</mtext>
          </mrow>
        </mrow>
      </mtd>
    </mtr>
    <mtr>
      <mtd>
        <mrow>
          <mrow>
            <maligngroup/>
          </mrow>
          <mrow>
            <maligngroup/>
            <mtext>(1)若</mtext>
            <mi mathvariant="normal">∀</mi>
            <msub>
              <mi>x</mi>
              <mrow>
                <mn>1</mn>
              </mrow>
            </msub>
            <mo>∈</mo>
            <mfenced open="[" close="]" separators="|">
              <mrow>
                <mi>a</mi>            
                <mo>,</mo>            
                <mi>b</mi>            
              </mrow>            
            </mfenced>
            <mo>,</mo>
            <mi mathvariant="normal">∀</mi>
            <msub>
              <mi>x</mi>
              <mrow>
                <mn>2</mn>
              </mrow>
            </msub>
            <mo>∈</mo>
            <mfenced open="[" close="]" separators="|">
              <mrow>
                <mi>c</mi>            
                <mo>,</mo>            
                <mi>d</mi>            
              </mrow>            
            </mfenced>
            <mo>,</mo>
            <mtext>总有</mtext>
            <mi>f</mi>
            <mfenced open="(" close=")" separators="|">
              <mrow>
                <msub>
                  <mi>x</mi>
                  <mrow>
                    <mn>1</mn>
                  </mrow>
                </msub>            
              </mrow>            
            </mfenced>
            <mo>&lt;</mo>
            <mi>g</mi>
            <mfenced open="(" close=")" separators="|">
              <mrow>
                <msub>
                  <mi>x</mi>
                  <mrow>
                    <mn>2</mn>
                  </mrow>
                </msub>            
              </mrow>            
            </mfenced>
            <mtext>成立,故</mtext>
            <mi>f</mi>
            <msub>
              <mfenced open="(" close=")" separators="|">
                <mrow>
                  <mi>x</mi>              
                </mrow>              
              </mfenced>
              <mrow>
                <mrow>
                  <mi mathvariant="normal">m</mi>
                  <mi mathvariant="normal">a</mi>
                  <mi mathvariant="normal">x</mi>
                </mrow>
              </mrow>
            </msub>
            <mo>&lt;</mo>
            <mi>g</mi>
            <msub>
              <mfenced open="(" close=")" separators="|">
                <mrow>
                  <mi>x</mi>              
                </mrow>              
              </mfenced>
              <mrow>
                <mrow>
                  <mi mathvariant="normal">m</mi>
                  <mi mathvariant="normal">i</mi>
                  <mi mathvariant="normal">n</mi>
                </mrow>
              </mrow>
            </msub>
            <mo>;</mo>
          </mrow>
        </mrow>
      </mtd>
    </mtr>
    <mtr>
      <mtd>
        <mrow>
          <mrow>
            <maligngroup/>
          </mrow>
          <mrow>
            <maligngroup/>
            <mtext>(2)若</mtext>
            <mi mathvariant="normal">∀</mi>
            <msub>
              <mi>x</mi>
              <mrow>
                <mn>1</mn>
              </mrow>
            </msub>
            <mo>∈</mo>
            <mfenced open="[" close="]" separators="|">
              <mrow>
                <mi>a</mi>            
                <mo>,</mo>            
                <mi>b</mi>            
              </mrow>            
            </mfenced>
            <mo>,</mo>
            <mi mathvariant="normal">∃</mi>
            <msub>
              <mi>x</mi>
              <mrow>
                <mn>2</mn>
              </mrow>
            </msub>
            <mo>∈</mo>
            <mfenced open="[" close="]" separators="|">
              <mrow>
                <mi>c</mi>            
                <mo>,</mo>            
                <mi>d</mi>            
              </mrow>            
            </mfenced>
            <mo>,</mo>
            <mtext>有</mtext>
            <mi>f</mi>
            <mfenced open="(" close=")" separators="|">
              <mrow>
                <msub>
                  <mi>x</mi>
                  <mrow>
                    <mn>1</mn>
                  </mrow>
                </msub>            
              </mrow>            
            </mfenced>
            <mo>&lt;</mo>
            <mi>g</mi>
            <mfenced open="(" close=")" separators="|">
              <mrow>
                <msub>
                  <mi>x</mi>
                  <mrow>
                    <mn>2</mn>
                  </mrow>
                </msub>            
              </mrow>            
            </mfenced>
            <mtext>成立,故</mtext>
            <mi>f</mi>
            <msub>
              <mfenced open="(" close=")" separators="|">
                <mrow>
                  <mi>x</mi>              
                </mrow>              
              </mfenced>
              <mrow>
                <mrow>
                  <mi mathvariant="normal">m</mi>
                  <mi mathvariant="normal">a</mi>
                  <mi mathvariant="normal">x</mi>
                </mrow>
              </mrow>
            </msub>
            <mo>&lt;</mo>
            <mi>g</mi>
            <msub>
              <mfenced open="(" close=")" separators="|">
                <mrow>
                  <mi>x</mi>              
                </mrow>              
              </mfenced>
              <mrow>
                <mrow>
                  <mi mathvariant="normal">m</mi>
                  <mi mathvariant="normal">a</mi>
                  <mi mathvariant="normal">x</mi>
                </mrow>
              </mrow>
            </msub>
            <mo>;</mo>
          </mrow>
        </mrow>
      </mtd>
    </mtr>
    <mtr>
      <mtd>
        <mrow>
          <mrow>
            <maligngroup/>
          </mrow>
          <mrow>
            <maligngroup/>
            <mtext>(3)若</mtext>
            <mi mathvariant="normal">∃</mi>
            <msub>
              <mi>x</mi>
              <mrow>
                <mn>1</mn>
              </mrow>
            </msub>
            <mo>∈</mo>
            <mfenced open="[" close="]" separators="|">
              <mrow>
                <mi>a</mi>            
                <mo>,</mo>            
                <mi>b</mi>            
              </mrow>            
            </mfenced>
            <mo>,</mo>
            <mi mathvariant="normal">∀</mi>
            <msub>
              <mi>x</mi>
              <mrow>
                <mn>2</mn>
              </mrow>
            </msub>
            <mo>∈</mo>
            <mfenced open="[" close="]" separators="|">
              <mrow>
                <mi>c</mi>            
                <mo>,</mo>            
                <mi>d</mi>            
              </mrow>            
            </mfenced>
            <mo>,</mo>
            <mtext>有</mtext>
            <mi>f</mi>
            <mfenced open="(" close=")" separators="|">
              <mrow>
                <msub>
                  <mi>x</mi>
                  <mrow>
                    <mn>1</mn>
                  </mrow>
                </msub>            
              </mrow>            
            </mfenced>
            <mo>&lt;</mo>
            <mi>g</mi>
            <mfenced open="(" close=")" separators="|">
              <mrow>
                <msub>
                  <mi>x</mi>
                  <mrow>
                    <mn>2</mn>
                  </mrow>
                </msub>            
              </mrow>            
            </mfenced>
            <mtext>成立,故</mtext>
            <mi>f</mi>
            <msub>
              <mfenced open="(" close=")" separators="|">
                <mrow>
                  <mi>x</mi>              
                </mrow>              
              </mfenced>
              <mrow>
                <mrow>
                  <mi mathvariant="normal">m</mi>
                  <mi mathvariant="normal">i</mi>
                  <mi mathvariant="normal">n</mi>
                </mrow>
              </mrow>
            </msub>
            <mo>&lt;</mo>
            <mi>g</mi>
            <msub>
              <mfenced open="(" close=")" separators="|">
                <mrow>
                  <mi>x</mi>              
                </mrow>              
              </mfenced>
              <mrow>
                <mrow>
                  <mi mathvariant="normal">m</mi>
                  <mi mathvariant="normal">i</mi>
                  <mi mathvariant="normal">n</mi>
                </mrow>
              </mrow>
            </msub>
            <mo>;</mo>
          </mrow>
        </mrow>
      </mtd>
    </mtr>
    <mtr>
      <mtd>
        <mrow>
          <mrow>
            <maligngroup/>
          </mrow>
          <mrow>
            <maligngroup/>
            <mtext>(4)若</mtext>
            <mi mathvariant="normal">∃</mi>
            <msub>
              <mi>x</mi>
              <mrow>
                <mn>1</mn>
              </mrow>
            </msub>
            <mo>∈</mo>
            <mfenced open="[" close="]" separators="|">
              <mrow>
                <mi>a</mi>            
                <mo>,</mo>            
                <mi>b</mi>            
              </mrow>            
            </mfenced>
            <mo>,</mo>
            <mi mathvariant="normal">∃</mi>
            <msub>
              <mi>x</mi>
              <mrow>
                <mn>2</mn>
              </mrow>
            </msub>
            <mo>∈</mo>
            <mfenced open="[" close="]" separators="|">
              <mrow>
                <mi>c</mi>            
                <mo>,</mo>            
                <mi>d</mi>            
              </mrow>            
            </mfenced>
            <mo>,</mo>
            <mtext>有</mtext>
            <mi>f</mi>
            <mfenced open="(" close=")" separators="|">
              <mrow>
                <msub>
                  <mi>x</mi>
                  <mrow>
                    <mn>1</mn>
                  </mrow>
                </msub>            
              </mrow>            
            </mfenced>
            <mo>&lt;</mo>
            <mi>g</mi>
            <mfenced open="(" close=")" separators="|">
              <mrow>
                <msub>
                  <mi>x</mi>
                  <mrow>
                    <mn>2</mn>
                  </mrow>
                </msub>            
              </mrow>            
            </mfenced>
            <mtext>成立</mtext>
            <mtext>故</mtext>
            <mi>f</mi>
            <msub>
              <mfenced open="(" close=")" separators="|">
                <mrow>
                  <mi>x</mi>              
                </mrow>              
              </mfenced>
              <mrow>
                <mrow>
                  <mi mathvariant="normal">m</mi>
                  <mi mathvariant="normal">i</mi>
                  <mi mathvariant="normal">n</mi>
                </mrow>
              </mrow>
            </msub>
            <mo>&lt;</mo>
            <mi>g</mi>
            <msub>
              <mfenced open="(" close=")" separators="|">
                <mrow>
                  <mi>x</mi>              
                </mrow>              
              </mfenced>
              <mrow>
                <mrow>
                  <mi mathvariant="normal">m</mi>
                  <mi mathvariant="normal">i</mi>
                  <mi mathvariant="normal">n</mi>
                </mrow>
              </mrow>
            </msub>
            <mo>;</mo>
          </mrow>
        </mrow>
      </mtd>
    </mtr>
  </mtable>
</math>

在WORD中可以直接CTRL+V成公式，相当方便！！！！！

• 上一篇
• 下一篇